다익스트라 알고리즘(Dijkstra Algorithm)은 어떤 변도 음수 가중치를 갖지 않는 유향 그래프에서 주어진 출발점과 도착점 사이의 최단 경로 문제를 푸는 알고리즘이다.
기본 로직은 출발점을 기준으로 연결되어 있는 정점들을 추가해가며, 최단 거리를 갱신하는 것이다.

위와 같은 그래프가 있다고 가정하며 출발점은 1번 정점이다.

이 중에서 경로가 가장 짧은 정점을 고르면 2, 3번 점이 된다.
2번 점부터 확인해보면, 2번 점의 최단 거리를 가지고 있는 현재 최단거리 (INF)와 1번 점의 최단거리(0) + 1~2번의 가중치(4) 값 중 가장작은 값으로 갱신한다. 코드로 만들면 다음과 같다. --> dist[2] = min(dist[2],dist[1]+adj[1][2])
따라서 min(INF, 4)이므로 4라는 값이 된다.
3번 점도 동일한 시행을 한다.

이제 나머지 정점 중에서 경로가 가장 짧은 정점을 고른다. 가장 짧은 거리를 가지고 있는 점은 가중치 2를 가지고 있는 3번 정점이다. 그리고 3번 정점에 인접한 노드는 4, 6번 정점이다.
4번 정점부터 확인해보면, 4번 정점의 최단 거리를 가지고 있는 현재 최단거리 (INF)와 3번 점의 최단거리(2) + 3~4번의 가중치(7) 값 중 가장 작은 값으로 갱신한다. --> dist[4]=min(dist[4],dist[3]+adj[3][4])
따라서 min(INF,9) 이므로 9라는 값이 된다.
반면 6번 정점은 dist[6] = min(dist[6],dist[3]+adj[3][6]) 으로 min(INF, 5)가 되어 5라는 값이 되는데
이중 더 작은 값인 6번 정점으로 가게된다.
근데 dist[4]는 9의 값이 아니다. 왜일까?
dist[4]로 오는 경로 중 vertex[1] --> vertex[2] --> vertex[4]가 있기 때문이다. 이 값은 5이므로 9보다 작다.
따라서 dist[4] = min(dist[4], dist[2]+adj[2][4]) 가 되어 5가 된다.
그럼 이제 dist[5]만 남았는데, dist[5]는 다음과 같다. dist[5] = min(dist[5], dist[2]+adj[2][5])
이 값은 min(INF, 4+2)가 되어 6이 된다.
최종적으로 dist[7]은 min(dist[7], dist[4]+adj[4][7], dist[5]+adj[5][7], dist[6]+adj[6][7]) 이 된다.
이 값은 min(INF, 8, 7, 10)이 되어 7이 된다.
이렇게 계속 적으로 반복하다 보면,
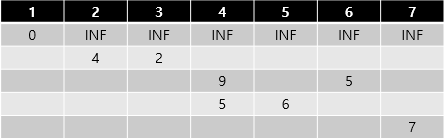
다익스트라 알고리즘을 적용한 최단 거리는 7이며 vertex[1] --> vertex[2] --> vertex[5] --> vertex[7]이 경로로 도착한다
'개발(Dev) 이야기 > Algorithm' 카테고리의 다른 글
| [BOJ] N과M(4)_15652.cpp (0) | 2020.03.17 |
|---|---|
| [BOJ] N과M(3)_15651.cpp (0) | 2020.03.17 |
| [BOJ] N과M(2)_15650.cpp (0) | 2020.03.17 |
| [BOJ] N과M (1)_15649.cpp (0) | 2020.03.17 |
| DFS(Depth-First Search)와 BFS(Breadth-First Search) (0) | 2019.08.11 |
